Model

Classification Report

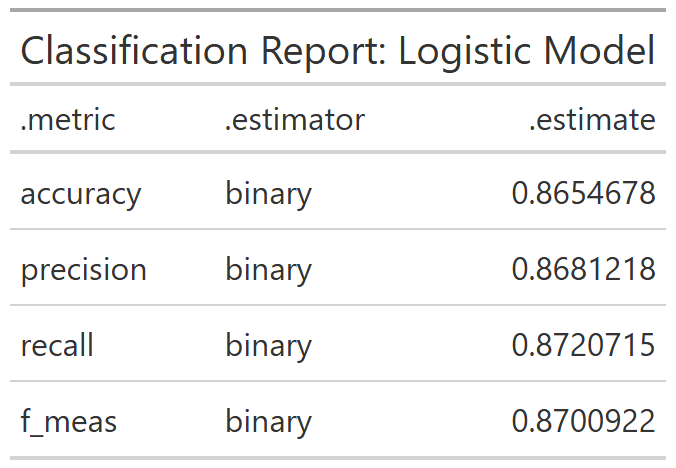
Logistic Regression Model

I tried to estimate the probability that White wins a game using the following logistic regression:

\[ \log \left( \frac{\Pr(\text{win\_bin}_i = 1)}{1 - \Pr(\text{win\_bin}_i = 1)} \right) = \beta_0 + \beta_1 \cdot \text{white\_elo}_i + \beta_2 \cdot \text{black\_elo}_i + \beta_3 \cdot \text{elo\_diff}_i + \beta_4 \cdot \text{opening\_prob}_i + \beta_5 \cdot \text{win\_rate}_i \]

Where:

• \(\text{win\_bin}_i\) = 1 if White wins game i, 0 otherwise
  
• \(\text{white\_elo}_i\) = Elo rating of the White player in game i
  
• \(\text{black\_elo}_i\) = Elo rating of the Black player in game i
  
• \(\text{elo\_diff}_i\) = Difference in Elo ratings: White Elo − Black Elo
  
• \(\text{opening\_prob}_i\) = Empirical win probability of the opening used in game i
  
• \(\text{win\_rate}_i\) = Mean historical win rate associated with the move pattern used in game i